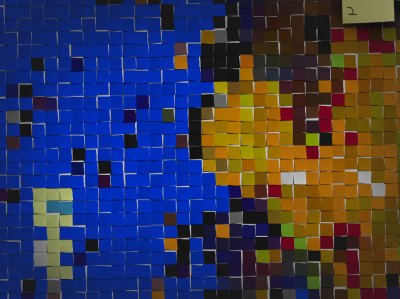“… no one, not even Benoit Mandelbrot himself […] had any real preconception of the set’s extraordinary richness. The Mandelbrot set was certainly no invention of any human mind. The set is just objectively there in the mathematics itself. If it has meaning to assign an actual existence to the Mandelbrot set, then that existence is not within our mind, for no one can fully comprehend the set’s endless variety and unlimited complication.”
Roger Penrose (from The Road to Reality)
The recent proliferation of 3D fractals, in particular the Mandelbox and Mandelbulb, got me thinking about the reality of these systems. The million dollar question is whether we discover or construct these entities. Surely these systems give the impression of exploring uncharted territory, perhaps even looking into another world. But the same can be said for many traditional man-made works of art.
I started out by citing Roger Penrose. He is a mathematical Platonist, and believes that both the fractals worlds (such as the Mandelbrot set) and the mathematical truths (such as Fermat’s last theorem) are discovered. In his view, the mathematical truths have an eternal, unchanging, objective existence in some kind of Platonic ideal world, independent of human observers.
In Penrose’s model, there are three distinct worlds: the physical world, the mental world (our perception of the physical world), and the cryptic Platonic world. Even Penrose himself admits that the connections and interactions between these worlds are mysterious. And personally I cannot see any kind of evidence pointing in favor of this third, metaphysical world.

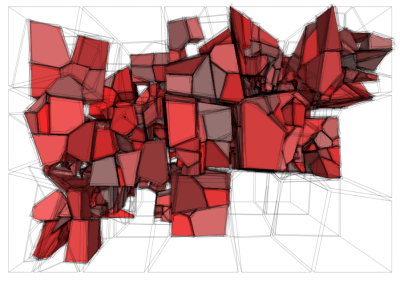
Designer World by David Makin
Roger Penrose is a highly renowned mathematician and physicist, and I value his opinions and works highly. In fact, it was one of his earlier books, The Emperors New Mind, that in part motivated me to become a physicist myself. But even though he is probably one of the most talented mathematicians living today, I am not convinced by his Platonist belief.
Personally, I subscribe to the less exotic formalist view: that the mathematical truths are the theorems we can derive by applying a set of deduction rules to a set of mathematical axioms. The axioms are not completely arbitrary, though. For instance, a classic mathematical discipline, such as Euclidean geometry, was clearly motivated by empirical observations of the physical world. The same does not necessarily apply to modern mathematical areas. For instance, Lobachevsky’s non-Euclidean geometry, was conceived by exploring the consequences of modifying one of Euclid’s fundamental postulates (interestingly non-Euclidean geometry later turned out to be useful in describing the physical world through Einstein’s general theory of relativity).
But if modern mathematics has become detached from its empirical roots, what governs the evolution of modern mathematics? Are all formal systems thus equally interesting to study? My guess is that most mathematicians gain some kind of intuition about what directions to pursue, based on a mixture of trends, historical research, and feedback from applied mathematics.

Mandelballs by Krzysztof Marczak [Mandelbox / Juliabulb mix]
Does my formalist position mean that I consider the Mandelbrot set to be a man-made creation, in the same category as a Picasso painting or a Bach concert? Not exactly. Because I do believe in a physical realism (in the sense that I believe in a objective, physical world independent of human existence), and since I do believe some parts of mathematics is inspired by this physical world and tries to model it, I believe some parts of mathematics can be attributed an objective status as well. But it is a weaker kind of objective existence: the mathematical models and structures used to describe reality are not persistent and ever-lasting, instead they may be refined and altered, as we progressively create models with greater predictive power. And I think this is the reason fractals often resemble natural structures and phenomena: because the mathematics used to produce the fractals was inspired by nature in the first place. Let me give another example:

Teeth by Jesse
Would a distant alien civilization come up with the same Mandelbrot images as we see? I think it is very likely. Any advanced civilization studying nature, would most likely have created models such as the natural numbers, the real numbers, and eventually the complex numbers. The complex numbers are extremely useful when modeling many physical phenomena, such as waves or electrodynamics, and complex numbers are essential in the description of quantum mechanics. And if this hypothetical civilization had computational power available, eventually someone would investigate the convergence of a simple, iterated system like z = z2 + c. So there would probably be a lot of overlapping mathematical structures. But there would also be differences: for instance the construction of the slightly more complex Mandelbox set contains several human-made design decisions, making it less likely to be invented by our distant civilization.
I think there is a connection to other areas of generative art as well. In the opening quote Penrose claims that no-one could have any real preconception of the Mandelbrot sets extraordinary richness. And the same applies to many generative systems: they are impossible to predict and often surprisingly complex and detailed. But this does not imply that they have a meta-physical Platonic origin. Many biological and physical systems share the same properties. And many of the most interesting generative systems are inspired by these physical or biological systems (for instance using models such as genetic algorithms, flocking behavior, cellular automata, reaction-diffusion systems, and L-systems).
Another point to consider is, that creating beautiful and interesting fractal images as the ones above, requires much more than a simple formula. It requires aesthetic intuition and skills to choose a proper palette, find an interesting camera location, and it takes many hours of formula parameter tweaking. I know this from my experiments with 3D fractals – I’m very rarely satisfied with my own results.
But to sum it all up: Even though fractals (and generative systems) may posses endless variety and unlimited complication, there is no need to call upon metaphysical worlds in order to explain them.