Category Archives: Fragmentarium

Distance Estimated 3D Fractals (Part VIII): Epilogue

Distance Estimation, Fractals, Fragmentarium

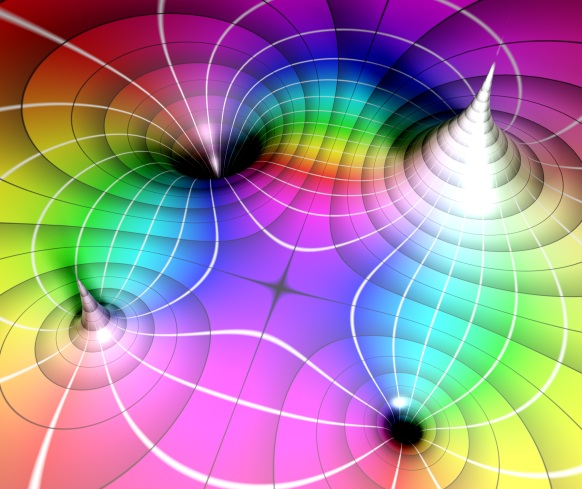
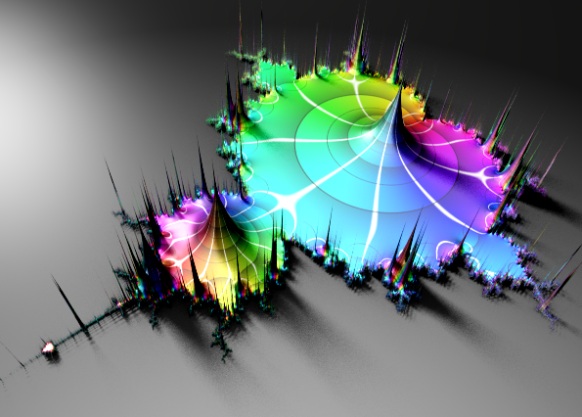
This is the last post in my introduction to distance estimated 3D fractals (see Part one for an overview). Originally, I intended this to be much shorter and more focused, but different topics kept sneaking up on me.

This final post discusses hybrid systems, and a few things that didn’t fit naturally in the previous posts. It also contains a small collection of links to relevant resources.

Hybrids

All the fractal systems mentioned in the previous parts apply the same transformation to each point for a number of iterations. But there is nothing that prevents applying different transformations at each iteration step. This has led to a number of hybrid systems, using building blocks from different fractals. They are very popular in Mandelbulb 3D, which comes with a huge library of transformations, which may be stringed together in a vast number of possible combinations.

Spudsville

It is difficult to trace the origin of many of these hybrids, since they are often cloned and modified. One of the more interesting base forms is the Spudsville system by Lenord (see also Hal Tenny’s tutorial on this system).

It is based on the following recipe:

5 x { Mandelbox, i.e. BoxFold, SphereFold, Scaling, Offset }
50 x {BoxFold, Mandelbulb power-2 Squaring }

Pseudo Kleinian

This is another popular base form, based on parameters from Theli-at’s Kleinian Drops. It is based on this formula:

12 x { Scale -1 Mandelbox }
1 x {BoxFold, Mandelbulb power-2 Squaring }
400 x { Scale 2 Mandelbox  }

A version of a similar system is available in Fragmentarium as “Knighty Collection/PseudoKleinian.frag”:

It is also possible to throw some Menger structure into the mix (see “Knighty Collection/PseudoKleinianMenger.frag”):

It is a very diverse system: this is the same formula, that I used as a base form for both Time Pieces:

and Pseudo-Kleinian Blue:

There really is no end to the possibilities. Here is another example:

where an octahedral symmetry transformation has been substituted in a Spudsville-like system:

7 x { Mandelbox, i.e. BoxFold, SphereFold, Scaling, Offset }
7 x { Octahedral, Mandelbulb power-2 Squaring }

The question is how to construct a suitable distance estimator for these hybrids systems. There is no easy answer to this. Mandelbulb3D and Mandelbulber both use the numerical gradient approximation discussed in part V of this series.

If the system is composed only of conformal transformations, the scalar approach discussed in part VI will be sufficient.

But for general combinations there is no easy way: it is often possible to guess a decent distance estimator, but more often than not, the analytic distance estimator overshoots and needs to be compensated by a fudge factor.

Interior renderings

The Mandelbrot distance estimation formula discussed in part V is only valid for exterior distances. There also exists a formula for the interior distance (for the 2D case), but it is much more complex than the exterior one, since it requires detecting cycles in the orbit.

However, in some cases the exterior distance estimate (or the absolute value of it), also works as an interior estimate (thanks to Visual for pointing this out). Here is an example of the interior of a Mandelbulb:

Geometric Orbit Trapping

Orbit trapping is often used to color fractals. During the orbit calculation the minimum distance to various geometric objects is stored (often the center, a sphere shell, or the x,y, and z-planes).

But it is also possible to use orbit traps to define the geometry of the fractals. Here is a standard Kaleidoscopic IFS like system, defined by DE such as:

float DE(vec3 z)
{
	int n = 0;
	while (n++ < Iterations) {
		// ...do some transformations here
		n++;
	}
	return length(z)*pow(Scale, float(-n));
}

resulting in an image like this:

but by inserting a trap-function and keeping the minimum value, we can create some interesting geometric variations:

float DE(vec3 z)
{
	int n = 0;
	float d= 1000.0;
	while (n++ < Iterations) {
		// ...do some transformations here
		n++;
		d = min(d,  trap(z) * pow(Scale, float(-n)));
	}
	return d;
}

for instance, using a cylinder-function for trap(z) results in an image like this:

Heightmap renderings

It is also possible to use distance estimated methods to draw heightmaps of fractals, e.g.:


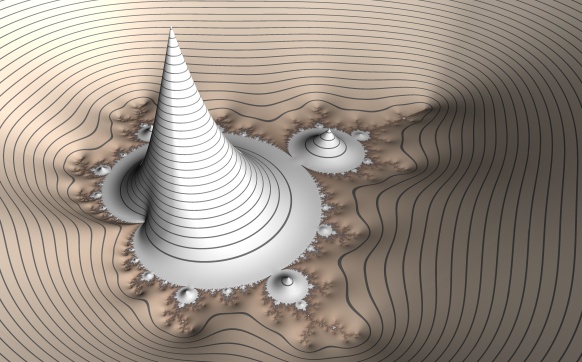
Included in Fragmentarium as 'Knighty Collection/MandelbrotHeightField.frag'

Or use heightmaps to visualize the algebraic structure of poles and zeroes in the complex plane:


Included in Fragmentarium as 'Experimental/LiftedDomainColoring3D.frag'

Heightmaps can also be generated from Perlin Noise, to create more realistic terrains:


Included in Fragmentarium as 'Experimental/Terrain.frag'

Knots, Polytopes, and Honeycombs

It is also possible to use distance estimation techniques to depict other mathematical structures than fractals. I've written about them before, but Knighty has explored DE's for knots and polyhedra:

for four-dimensional polychora:

and even for hyperbolic honeycombs:

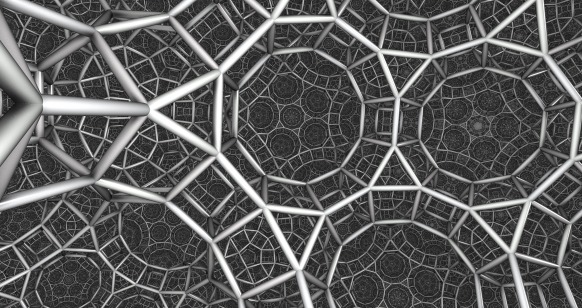
(There are several examples included with Fragmentarium)

Resources

Software

The easiest way to start exploring 3D fractals is probably by trying Mandelbulb 3D or Mandelbulber. Both are very powerful and feature-rich applications.

Mandelbulb 3D (by Jesse) is probably the most used 3D fractal creation tool (judging by pictures posted at Fractal Forums). It contains many different formulas and fragments, which can be combined as hybrids. It is free, closed-source, CPU-based, and Windows only.

Mandelbulber (by Buddhi) is open source, and available for Windows, Linux, and Mac. CPU-based, but with OpenCL preview!

GPU Based renderers

Fragmentarium is my own playground for working with GPU (GLSL) based pixel graphics. It is meant to create a modular and interactive environment for working with 2D and 3D graphics. All the images in this series of blog post were made with Fragmentarium, and many of the systems are included as examples.

Rrrola's Boxplorer is a fast interactive Mandelbox explorer. It has been extended by Marius Schilder in Boxplorer2 to include spline animations, stereo view, and many examples of fractal systems.

Subblue's Pixel Bender Mandelbulb script was one of the first GPU implementations. He has made many great fractal animations and images, so be sure to visit his web site. He also created the impressive Fractal Lab WebGL site, which made it possible to explore fractals directly in a browser (the site is currently under reconstruction)

Eiffie's Animandel Pro is a tool for creating fractal animations. It features a GLSL editor and even an integrated C-compiler for dynamically compiled CPU code. It is certainly not the easiest way to get started, but as can be seen from Eiffie's videos it is a powerful tool.

Web sites and papers

Fractal Forums is the place, where all the new development and discoveries can be followed. It's a treasure chest filled with information, but it can be difficult to find it in the archives. A good place to start is the original Mandelbox thread and the thread about DE's for the Mandelbox.

Daniel White’s Mandelbulb site is probably the best account of the history of this fractal. Also see Paul Nylander’s Hypercomplex systems.

Tom Lowe's Mandelbox site has a lot of information on the Mandelbox, collected by the person who discovered it himself.

Hypercomplex Iterations: Distance Estimation and Higher Dimensional Fractals (2002). by Dang, Kaufmann, and Sandin is a rare mathematical treatment of higher-dimensional fractals and their distance estimates. It is free (but tough!).

J. C. Hart's original paper Ray tracing deterministic 3-D fractals and his sphere tracing papers are must-reads. He has also written many other great papers.

Pouet.net is a web site for demo scene coders. There is a strong emphasis on heavily optimized and efficient code. Several demos features distance estimation and fractals.

In particular Iñigo Quílez has explored fractals and distance fields in a demo scene context. His Rendering Worlds With Two Triangles is a good introduction to distance field rendering. But be sure to check out Quilez's website - there is an abundance of good stuff, including lots of tutorials.

Fragmentarium 0.9.1 (“Chiaroscuro”) Released

Fragmentarium

I’ve released a new build of Fragmentarium, version 0.9.1 (“Chiaroscuro”).
It can be downloaded at Github (as of now only Windows builds are available).

The usual caveats apply: Fragmentarium is very much work in progress, and is best suited for people who like to experiment with code.

Dual buffers

The main new feature is support for dual buffers and dual shaders. The front buffer is swapped after each frame to the backbuffer, which can be accessed as: ‘uniform sampler2D backbuffer;’.

Buffers can be created as either 8-bit or 16-bit integer, or 32-bit float. The new buffers makes it possible to create accumulated ray tracing, high quality AA for 2D systems, and many types of feedback systems. The easiest way to start exploring these features is by looking at the new tutorials (see below).


Minor improvements:

  • Changed UI a bit to make it easier to change from automatic to continuous rendering.
  • Added context menu option to insert preset based on current settings.
  • The syntax for using ‘2D.frag’ is simpler now. Just implement: “vec3 color(vec2 c);”
  • Bugfix: Fixed error in 2D.frag, where changing aspect ratio would mess up viewport translation.
  • Bugfix: Fixed some errors in the included fragments: Noise, Tetrahedron, and several of Knighty’s examples were missing a ‘providesInit’.
  • Bugfix: Fixed specular bug in standard-raytracer.
  • Bugfix: Copying from web was sometimes weird (should now strip rich text).
  • Bugfix: Autosave files now creates a directory with output files (necessary since the #BufferShader directive broke the old ‘include all in one file’ system).


New fragments:

  • Added a new ‘tutorial’ category, with examples of many features in Fragmentarium.
  • Soft-Raytracer.frag – An example progressive (accumulated) ray-tracer. DOF using finite aperture, HDR and tonemapping, soft shadows, and multiple ray ambient occlusion, and sub-pixel jittered high-quality anti-alias. All very experimental.
  • Progressive2D.frag, Progressive2DJulia.frag – Can be used for high-quality (progressive) anti-alias of 2D systems. Uniform disk sampling, Gaussian and Box filtering, “gamma correct” averaging of samples.
  • A Quilez inspired ‘Domain Distortion’ example.
  • A dual-buffered Game of Life example.
  • Mandelbrot Averaged Stripe Coloring example.
  • Lifted Domain Coloring example (in 2D/3D), see here.
  • New ‘Theory’ category with examples of the dual number and automatic differentiation method.
  • Some great new scripts from Knighty, for polyhedrons, knots, polychora, and hyperbolic tesselations. See here and here.

ATI users

Some fragments fail on ATI cards. This seems to be due to faulty GLSL driver optimizations. A workaround is to lock the ‘iterations’ variable (click the padlock next to it). Adding a bailout check inside the main DE loop (e.g. ‘if (length(z)>1000.0) break;’) also seems to do the job. I don’t own an ATI card, so I cannot debug this without people helping.

Mac users

Some Mac users has reported problems with the last version of Fragmentarium. Again, I don’t own a Mac, so I cannot solve these issues without help.

Finally, please read the FAQ, before asking questions.

For more examples of images generated with the new version, take a look at the Flickr Fragmentarium stream.

Spherical Worlds

Fractals, Fragmentarium

Recently I saw a description of spherical fractals in a blog post by Samuel Monnier.

These Julia-sets are constructed like ordinary Mandelbrots and Julias: first the argument is squared, but instead of adding a constant afterwards, a Möbius transformation is applied:

\(z = \frac{a z^2 + b}{c z^2 + d}\)

For the right choices of (complex) constants, plane-filling patterns appear.

There is an intimate connection between Möbius transformations and spherical geometry: if the plane is stereographically projected onto a sphere, a Möbius transformations corresponds to rotating and moving the sphere, and then project stereographically back to the plane (this is nicely visualized in this video).



This connection can be visualized graphically: if the plane-filling patterns are stereographically projected onto a sphere, they fit naturally on it. There are no discontinuities or voids, and no singularities near the poles.



Here I’ve used Fragmentarium to create some images of these plane-filling patterns, together with their stereographical projection onto a sphere. It was done by distance estimated ray marching, but in this case we could have used ordinary ray tracing, and calculated the exact intersections.



The Fragmentarium script can be found here.

Lifted Domain Coloring

Fractals, Fragmentarium, Mathematical Art

This year, one of the pictures at the International Science & Engineering Visualization Challenge, caught my interest.

Poelke and Polthier’s Lifted Domain Coloring is a coloring scheme for visualizing properties of complex functions: it maps numbers in the complex plane stereographically to the Riemann sphere, and assigns a hue based on the inclination angle (though I’m not sure that much is gained by the stereographic projection, since the polar representation of the complex numbers seems to provide all the needed information). Saturation and Brightness are controlled by the modulus of the number: when the modulus goes towards infinity, the color turns white, and for numbers close to zero, the color turns black. The exact radial mapping used by the authors is not specified in the paper, but I think my implementation is quite close:

The visualization scheme makes it possible to visually identify different properties, such as zeroes and poles in complex functions.

One of the ways, I think such a visualization may be improved is by using a heightmap:

Here I’ve raised the poles and lowered the zeroes: first, I made the poles and zeroes appear symmetric, by transforming the modulus: r = abs(r + 1/r). Then I applied a sigmoid function to tame the infinities, and finally another sigmoid transformation was applied to change the sign of the zeroes. This technique will only work for somewhat well-behaved functions (meromorph functions – functions with a countable number of zeroes and poles).

Of course, I’ve also tested the Lifted Domain Coloring scheme on fractals.

Here is a Mandelbrot and Julia plot:

Usually Mandelbrot visualizations focus on coloring the outside of the set, but since the exterior of the Mandelbrot set has infinite modulus, only the interior (with its zeroes) are visualized here. The zeroes are visualized as peaks for better graphical clarity.

I also tested the coloring scheme on Samuel Monnier’s Ducks fractal:


Here, the coloring scheme does a decent job for low iteration counts, but for higher iterations the images become messy, so for pure aestethic purposes there are probably better coloring schemes around.

Distance Estimated Polychora

Distance Estimation, Folding, Fragmentarium, Mathematical Art

My last post mentioned some scripts that Knighty (a Fractal Forums member) made for distance estimated rendering of many types of polyhedra, including the Platonic solids. Shortly after, Knighty really raised the bar by finding a distance estimator for four dimensional polytopes. In this post, I’ll show some images of a subset of these, the convex regular polychora.

There are several ways to depict four dimensional structures. The 4D Quaternion Julia, one of the first distance estimated fractals, simply showed 3D slices of 4D space. Another way would be to project the shadow of a 4D object onto a 3D space. Ideally, a proper perspective projective would be preferable, but this seems to be complicatated with distance estimation techniques.

The technique Knighty used to create a 3D projection, was to place the polychoron boundary on a 3-sphere, and then stereographically project the 3-sphere surface onto a 3-dimensional space. For a very thorough and graphical introduction to stereographic projection of higher-dimensional polytopes, see this great movie: Dimensions. It should be noted that the Jenn3D program also uses this projection to depict a variety of polytopes (using polygonal rendering, not distance estimated ray marching).

Back to the structures:

The convex regular 4-polytopes are the four-dimensional analogs of the Platonic solids. They are bounded by three-dimensional cells, which are all Platonic solids of the same kind (similar to the way the Platonic solids are bounded by identical regular 2D polygons). The convex regular polytopes are consistently named by the number of identical cells (Platonic solids) that bounds them. In four dimensions, there are six of these, one more than the number of Platonic solids.

5-cell

The 5-cell (or 4-simplex, or hypertetrahedron) is the simplest of the convex regular polytopes. It is composed of 5 three-dimensional tetrahedrons, resulting in a total of 5 vertices and 10 edges. It is the 4D generalisation of a tetrahedron.

The curved lines are a consequence of the stereographic projection. In 4D the lines would be straight.

8-cell

The 8-cell (or hypercube, or Tesseract) is also simple. Composed of 8 3D-cubes, it has 16 vertices, and 32 edges. It is the 4D generalisation of a cube.

16-cell

Things start to get more complicated with the 16-cell (or hyperoctahedron). It is composed of 16 tetrahedrons, and has 8 vertices and 24 edges. It is the 4D generalisation of an octahedron.

Notice, that if we rotate the 3-sphere, we can get interesting depictions, with edges getting infinitely long in 3-space:

24-cell

The 24-cell is exceptional, since it has no 3D analogue. It is built from 24 octahedrons, has 24 vertices and 96 edges.

120-cell

The 120-cell is a beast, built from 120 three-dimensional dodecahedra. With 600 vertices and 1200 edges, it is the most complex of the convex, regular polychora. It is the 4D generalisation of a dodecahedron.

Zooming in, it is easier to see the pentagons making up the dodecahedra.

600-cell

Finaly, the 600-cell is built from an even larger number of polyhedra: 600 three-dimensional tetrahedrons. However, the simpler polyhedra means there is only a total of 120 vertices and 720 edges. It is the 4D generalisation of an icosahedron.

Knighty’s great Fragmentarium scripts can be found in this thread at Fractal Forums.

Knighty’s script is not limited to regular convex polychora. Many types of polytopes can be made. Here are the parameters used for the images in this post:

polychora06.frag parameters:

Type,U,V,W,T
3,0,1,0,0 - 5-cell
4,0,1,0,0 - 8-cell
4,0,0,1,0 - 24-cell
4,0,0,0,1 - 16-cell
5,0,1,0,0 - 120-cell
5,0,0,0,1 - 600-cell

And for completeness, here are the parameters for the 3D polyhedron script:

Type,U,V,W
3,0,1,0 Tetrahedron
4,0,0,1 Cube
3,1,0,0 Octahedron
5,0,0,1 Dodecahedron
5,0,1,0 Icosahedron

Knots and Polyhedra

Fragmentarium, Raytracing

Over at Fractal Forums, DarkBeam came up with a Distance Estimator for a trefoil knot in this thread. Here are a few samples, created using the new ‘soft’ raytracer, I’m working on in Fragmentarium:

These kinds of knots are easy to describe by a parametrized curve, but making a distance estimator for them is impressive – I wouldn’t have guessed it was possible at all.

It is also possible to create several variations:

In the same thread, Knighty came up with an impressive figure-8 knot distance estimator:

In another thread at Fractal Forums, Knighty also published an interesting technique (“Fold and Cuts”) for creating a large variety of distance estimated polyhedra:

(If you wonder about the materials, I’ve added some 3D Perlin noise to the distance estimate – this is simple way to creature a structural texture, and it creates true displacements, not just surface normal perturbations).

The threads linked to above contains Fragmentarium scripts with the relevant distance estimators.

Fragmentarium FAQ

Fragmentarium, GPU

Here is a small collection of questions, I’ve have been asked from time to time about Fragmentarium.

Why does Fragmentarium crash?

The most common cause for this is, that a drawing operation takes too long to complete. On Windows, there is a two seconds maximum time limit on jobs executing on the GPU. After that, a GPU watchdog timer will kill the graphics driver and restore it (resulting in unresponsive, possible black, display for 5-10 seconds). The host process (here Fragmentarium) will also be shut down by Windows.

If this happens, you will get errors like this:

"The NVIDIA OpenGL driver lost connection with the display driver
and is unable to continue. 
The application must close.... Error code: 8"
"Display driver stopped responding and has recovered"

Workarounds:
Try lowering the number of ray steps, the number of iterations or use the preview feature. Notice that for high-resolution renders, the time limit is for each tile, so it is still possible to do high resolution images.

Another solution is to change the watchdog timer behaviour via the TDR Registry Keys:

The TDR registry keys were not defined in my registry, but I added a 

DWORD TdrDelay = 30

and a 

DWORD TdrDdiDelay = 30

key to 

HKEY_LOCAL_MACHINE\System\CurrentControlSet\Control\GraphicsDrivers

which sets a 30 second window for GPU calculations. You have to restart Windows to apply these settings. Be advised that changing these settings may render your system completely unresponsive if the GPU crashes.

Why does Fragmentarium not work on my GPU?

Even though GLSL is a well-defined standard, the are differences between different vendor implementations and different drivers. The computers I have use have Nvidia cards, so Fragmentarium is most tested on Nvidia’s platform.

Typical problems:

The ATI compiler is more strict about casting. For instance, adding an integer to a float results in an error, and not in a warning:

float a = b + 3;

The ATI compiler also seems to suffer from some loop optimization problems: some of the fractals in Fragmentarium does not work on my ATI card, if the number of iterations is not locked (or hard-coded in the fragment code). Inserting a condition into the loop also solves the problem.

The Intel GPU compiler also has some issues: for instance, some operations on literal constants results in errors:

vec3 up = normalize(vec3(1.0,0.0,0.0)); // fails on Intel

I get weird errors about disabled widgets?

If you see warnings like:

Unable to find 'FloorNormal' in shader program. Disabling widget.

it does not indicate a problem. For instance, the warning above appears when the EnableFloor checkbox is locked and disabled. In this case, the GLSL will optimize the floor code away, and the FloorNormal uniform variable will no longer be part of the compiled program – hence the warning. These warnings can be safely ignored.

Why does your Fragmentarium images look much nicer than the ones I get in Fragmentarium?

The images I post are always rendered at a higher resolution using the High Resolution Render option. I then downscale the images to a lower resolution. This reduces alias and rendering artifacts. Use a painting program with a proper downscaling filter – I use Paint.NET which seems to work okay.

Before rendering in hi-res, use the Tile Preview to zoom in, and adjust the details level and number of ray steps, so the image looks okay in the Tile Preview resolution.

Why is Fragmentarium slower than BoxPlorer/Fractals.io/…?

The default ray tracer in Fragmentarium has grown somewhat complex. It is possible to gain speed by locking variables, but this is somewhat tedious. Another solution is to change to another raytracer, e.g. change

#include "DE-Raytracer.frag"

to either 

#include "Fast-Raytracer.frag"

(a faster version of the ones above, which will remember all settings)

or 

#include "Subblue-Raytracer.frag"

(Tom Beddards raytracer, which uses a set of different parameters)

Can I use double precision in my shaders?

Most modern graphics cards support double precision numbers in hardware, so in principle, yes, if your card supports it. In practice, it is much more difficult:

First, the Fragmentarium presets and sliders (including camera settings), will only transfer data (uniforms) to the GPU as single precision floats. This is not the biggest problem, since you might only need double precision for the numbers that accumulate errors. The Qt OpenGL wrappers I use doesn’t support double types, but it would be possible to work around this if needed.

Second, while newer GLSL versions do support double precision numbers (through types such as double, dvec3, dmat3), not all of the built-in functions support them. In particular, there are no trigonometric or exponential functions. So no cos(double), exp(double), etc. The available functions are described here.

Third, it might be slow: When Nvidia designed their Fermi architecture, used in their recent graphic cards, they built it, so that is should be able to process double precision operations with half the speed of single precision operations (which is optimal given the double size of the numbers). However, they decided that their consumer branch (the Nvidia cards) should be artificially limited to run double precision calculations at 1/8 the speed of single precision numbers. Their Tesla line of graphics card (which shares architecture with the Geforce branch), is not artifically throttled and will run double precision at half the speed of single precision. As for the AMD/ATI cards, I do not think they have similar limitations, but I’m not sure about this.

If you really still want to try, you must insert this command at the top of the script:

#extension GL_ARB_gpu_shader_fp64 : enable

(Or use a #version command, but this will like cause problems with most of the existing examples).

Finally, what about emulating double precision numbers, instead of using the hardware versions? While this sounds very slow, it is probably not much slower than the throttled implementation. The downside is, the GLSL does not support operator overloading: there is no syntactically nice way to implement such functionality: instead of just changing your data types, you must convert all code from e.g. 

A = B*C+D;

to 

A = dplus(dmul(B,C),D);

If you are still interested, here is a great introduction to emulating doubles in GLSL.

How do I report errors, so that it is easiest for you to correct them?

(Well, actually nobody asks this questions)

If you find an error, please report the following:
– Operating system, and the graphics card you are using
– The version of Fragmentarium, and whether you built it yourself
– A reproducible description of the steps that caused the error (if possible).

You may mail errors to me at mikael (at) hvidtfeldts.net.

Fragmentarium 0.9 Released

Fractals, Fragmentarium

I’ve released a new build of Fragmentarium, version 0.9 (“Sun Ra”).

Download at Github.
(As of now only Windows builds are available)

New features

  • New high resolution output dialog (with auto-naming and auto-backup of scripts and parameters)
  • Locking of parameters (makes rendering considerably faster in some cases by turning uniforms into constants)

Minor improvements

  • Mouse wheel now changes camera position, not FOV
  • Default raytracer improvements:
    • Removed ‘AntiAliasBlur’,’MaxRayStepDiv’, and ‘NormalDetail’ settings
    • Added reflection
    • Shadows (hard, and pseudo-soft shadows)
    • Added dithering (for banding removal) and very simple RNG functionality.
    • Added new ambient occlusion method (similar to Rrola/Subblue – sample along normal for proximity).
  • Added a simpler, but faster version of my raytracer. Just include “Fast-Raytracer.frag” instead of “DE-Raytracer.frag”
  • Added a port of Subblues Fractal Labs (fractal.io) raytracer (GPL). Just include “Subblue-Raytracer.frag” instead of “DE-Raytracer.frag”
  • Added vertical scroll bars to user parameter groups.
  • Added ‘#define providesInit’, ‘#define providesColor’ (to provide custom coloring)
  • Added vec4 GUI slider type
  • Now disables uniforms which are not used in shader.
  • Compiler warnings are now shown in output, also if there is no errors.
  • Bugfix: resize of window now updates aspect ratio.
  • Bugfix: handling of specular exponent = 0
  • BugFix: fixed fps timer for >500ms renders
  • BugFix: Tile Render now works in manual mode.
  • BugFix: Using mouse and key movement at the same time, would result in distance between eye and target getting smaller and smaller.

New fragments

  • A whole collection of new fragments from Knighty!
  • Some of my own new fragments: GraphPlotter, KaliSet, BurningShip, Spudsville, Mandelbrot2D, Terrain.
  • 2DJulia.frag and Complex.frag to make 2D fractals easier.
  • New raytracers: Subblue-Raytracer.frag, Fast-Raytracer.frag
  • QuilezLib with Iñigo Quilez’s collection of sphere tracing primitives
  • Ashima-Noise.frag, a library of Noise functions.

Comments

Some of the new utility libraries make fractals very easy to explore. For instance, 2D escape time fractals are very easy to explore now.

Here is an example:

#include "2DJulia.frag"
#include "Complex.frag"

// 'Ducks' fractal by Samuel Monnier
vec2 formula(vec2 z, vec2 c) {
    return cLog(vec2(z.x,abs(z.y)))+c;
}

which produces this:

Other examples:


Terrain example – example of the new noise library


Mandelbrot heightmap example – based on Knighty’s example

For more example of images generated with the new version, take a look at the Flickr Fragmentarium stream.

Notice for ATI users

Several fragments fail on ATI cards. This seems to be due to faulty GLSL driver optimizations. A workaround is to lock the ‘iterations’ variable (click the padlock next to it). Adding a bailout check inside the main DE loop (e.g. ‘if (length(z)>1000.0) break;’) also seems to do the job.