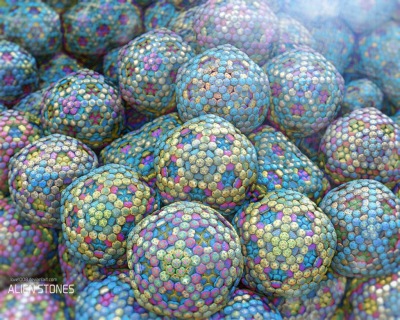Category Archives: Kaleidoscopic IFS

Hybrid 3D Fractals

Fractals, Fragmentarium, Kaleidoscopic IFS, Mandelbulb

A lot of great images have been made of the Mandelbulb, the Mandelbox, and the various kaleidoscopic IFS’s (the non-platonic non-solids). And it turns out that by combining these formulas (and stirring a few assorted functions into the mix), a variety of new, amazing, and surprising forms emerge.

I’m currently working on making it easier to combine different formulas in Fragmentarium – but until I get something released, here is a collection of images and movies created by Mandelbulb 3D (Windows, free) and Mandelbulber (Windows, free, open-source), that illustrates the beauty and diversity of these hybrid systems. Be sure to view the large versions by following the links. The images were all found at Fractal Forums.

Videos


Buddhi – Mandelbox and Flying Lights


Jérémie Brunet (Bib) – Weird Planet II


Jérémie Brunet (Bib) – Like in a dream II

Images


Lenord – Pray your Gods


Tomot – It’s a jungle out there


Lenord – J.A.R.


MarkJayBee – Security Mechanisms


Fractal00 – Alien Stones


Kr0mat1k – Restructuration


BrutalToad – Jülchen

Written Images

Cinder, Folding, Generative Art, Kaleidoscopic IFS

Written Images is a generative book with artworks from different artists. All images are unique, created on-demand, when a new copy of the book is printed. 70 applications were submitted (see the overview video), and a jury selected 42 of these for the final collection.

Some of the submissions that caught my eye:

Cindermedusae

First, I think Marcin Ignac’s Cindermedusae is an amazing work. He generates imaginary sea creatures in the style of Ernst Haeckel.

Cindermedusae was created in Cinder and OpenGL, and generates images in near-realtime (one of the requirements for Written Images was a maximum calculation time of 15 seconds).

Division

W:Blut created Division for Written Images. It seems to be created using his interesting Hemesh library for Processing.

Origami Butterfly

Jonathan McCabe contributed with the Origami Butterfly. His images are created using an iterated folding process in 2D – which is interesting, because the Kaleidoscopic Iterated Functions Systems and the Mandelbox use a similar approach, but in 3D.

The Origami Butterfly process is described in a bit more detail at this post at Generator.x.

Jacob’s Cave

Jacob’s cave is made by Sansumbrella, created using Cinder. Intriguing complex shapes, yet very simple and elegant:

Folding Space II: Kaleidoscopic Fractals

Fractals, GPU, Kaleidoscopic IFS, Mandelbulb

Another type of interesting 3D fractal has appeared over at fractalforums.com: the Kaleidoscopic 3D fractals, introduced in this thread, by Knighty.

Once again these fractals are defined by investing the convergence properties of a simple function. And similar to the Mandelbox, the function is built around the concept of folds. Geometrically, a fold is simply a conditional reflection: you reflect a point in a plane, if it is located on the wrong side of the plane.

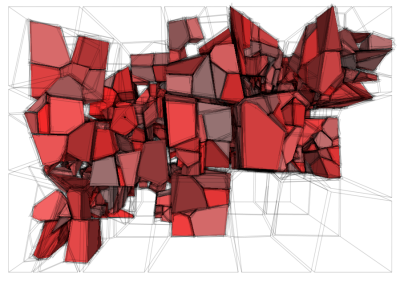
It turns out that just by using plane-folds and scaling, it is possible to create classic 3D fractals, such as the Menger cube and the Sierpinsky tetrahedron, and even recursive versions of the rest of the Platonic solids: the octahedron, the dodecahedron, and the icosahedron.


Example of a recursive dodecahedron

The kaleidoscopic fractals introduce an additional 3D rotation before and after the folds. It turns out that these perturbations introduce a rich variety of interesting and complex structures.

I’ve followed the thread and implemented most of the proposed systems by modifying Subblue’s Pixel Bender scripts.

Below are some of my images:

The Menger Sponge

My first attempts. Pixel Bender kept crashing on me, until I realized that there is a GPU timeout in Windows Vista (read this for a solution).


The Sierpinsky

Then I moved on to the Sierpinsky. The sequence below shows something characteristic for these fractals: the first slightly perturbed variations look artificial and synthetic, but when the system is distorted, it becomes organic and alive.



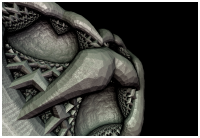
The Icosahedron

I also tried the octahedron and dodecahedron, but my favorite is the icosahedron. Especially knighty’s hollow variant.




Arbitrary Planes

One nice thing about these systems is, that you do not necessarily need to derive a complex distance estimator – you can also just modify the distance estimator code, and see what happens. These last two images were constructed by modifying existing distance estimators.

It will be interesting to see where this is going.

Many fascinating 3D fractals have appeared at fractalforums.com over the last few weeks. And GPU processing now makes it is possible to explore these systems in real-time.